Stochastic Gradient Descent

1. Gradient Descent

이전까지 다루었던 Tabular Reinforcement learning의 단점 때문에 function approximator를 도입하게 되었고 value function을 w라는 parameter를 통해서 approximate하였습니다. 또한 이제 학습이라는 것은 이 paramater를 update하는 것이라고 했었습니다.

그렇다면 parameter를 update를 하는 것은 어떻게 할 수 있을까요? 이전에 machine learning에 대해서 접해본 분이면 잘 아는 Stochastic Gradient Descent방법을 활용하여 value function의 parameter를 update하게 됩니다. 이 방법은 간단하면서도 간단하기 때문에 프로그램 상으로 강력한 update방법입니다. 하지만 시작점에서 조금만 달라져도 다른 극점에 도착할 수 있으며 도착한 극점은 global optimum이 아닐수도 있습니다. 이러한 단점을 극복하는 방법은 여러가지가 있지만 처음 parameter를 update하는 것을 배우는 입장에서는 간단한 개념을 알고 나중에 활용할 때 그러한 기법들을 도입하면 될 것 같습니다. 개념은 다음과 같습니다. w로 표현하는 함수, 여기서는 J(w)로 표현한 함수는 어떠한 update의 목표로서 보통은 내가 원하는 대상과 자신의 error로 설정해서 그 error를 최소화하는 것을 목표로 합니다. update를 하려면 어느방향으로 가야 그 error가 줄어드는 지 알아야하는 데 그것을 함수의 미분(gradient)을 취해서 알 수 있습니다. gradient자체는 경사이기 때문에 곡면에서 보자면 위로 올라가는 방향이므로 -를 곱해서 그 반대 방향으로 내려감으로서(descent) 조금씩 error를 줄여나가는 것입니다.

2. Example

gradient descent에 대한 위키페이지는 다음과 같습니다.https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95

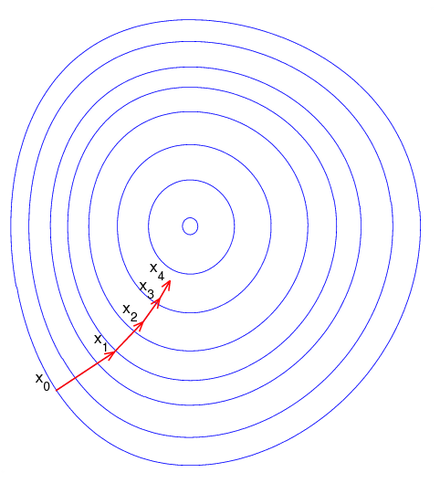
아래의 그림을 어떠한 함수의 parameter space라고 하면 $$x_0$$부터 시작해서 함수의 gradient를 따라서 점진적으로 가운데의 극점으로 내려가게 됩니다. 언덕에서 공을 굴려서 아래로 떨어지고 있다고 생각하면 자연스로 경사를 따라서 내려가는 형태와 비슷합니다.

실제로 어떤 함수의 극점을 구하는 것을 방정식의 해를 구하는 방법이 아닌 numerical하게 풀어보는 예는 아래와 같습니다. 간단히 Stochastic gradient descent의 방법을 보여주는 코드도 있습니다.

Gradient Descent on RL

Gradient의 개념을 살펴보았습니다. 이 개념을 강화학습에 적용시켜보도록 하겠습니다. 강화학습에서는 J(w)를 어떻게 정의할까요? 바로 true value function과 approximate value $$\hat{v}(s,w)$$와의 error로 잡습니다.

Gradient Descent방법도 (1) Stochastic Gradient Descent(SGD)와 (2) Batch방법으로 나눌 수 있는데 위와 같이 모든 state에서 true value function과의 error을 한 번에 함수로 잡아서 업데이트하는 방식은 Batch의 방식을 활용한 것으로서 step by step으로 업데이트하는 것이 아니고 한 꺼번에 업데이트하는 것입니다. Mean-spuared error를 gradient방식에 집어넣어서 gradient를 취해보면 아래와 같습니다.

하지만 DP에서 강화학습으로 넘어갈 때처럼 expectation을 없애고 sampling으로 대체하면 아래와 같아집니다.

이전에 MC와 TD Learning에서 했듯이 True value function 부분을 여러가지로 대체할 수 있습니다. Sample Return을 사용할 수도 있고 TD target을 사용할 수도 있습니다.