TD Prediction
Last updated
Last updated
이전 chapter에서 배웠던 Monte-Carlo Control은 Model-Free Control입니다. Model-Free라는 점에서 강화학습이지만 단점이 있습니다. 바로 online으로 바로바로 학습할 수가 없고 꼭 끝나는 episode여야 한다는 단점이 있습니다. 끝나지 않더라도 episode가 길 경우에는(예를 들어 atari게임이 아니라 starcraft같은 게임) 학습하기 어려운 단점이 있습니다. 따라서 자연스럽게도 꼭 episode가 끝나지 않더라고 DP처럼 time step마다 학습할 수 있지 않나?라는 생각을 하게 됩니다. 이게 바로 Temporal Difference이며 Sutton교수님 책에서는 아래와 같이 소개하고 있습니다.
If one had to identify one idea as central and novel to reinforcement learning, it would undoubtedly be temporal-difference (TD) learning. TD learning is a combination of Monte Carlo ideas and dynamic programming (DP) ideas. Like Monte Carlo methods, TD methods can learn directly from raw experience without a model of the environment's dynamics. Like DP, TD methods update estimates based in part on other learned estimates, without waiting for a final outcome (they bootstrap)
Temporal difference(TD)는 MC와 DP를 섞은 것으로서 MC처럼 raw experience로부터 학습할 수 있지만 DP처럼 time step마다 학습할 수 있는 방법입니다. 마지막에 "bootstrap"이라고 하는데 이 말은 무엇을 뜻할까요?
대학생활을 예로 들어보겠습니다. MC는 대학교에 들어와서 졸업을 한 다음에 그 동안을 돌아보며 "이건 더 했어야했고 술은 덜 마셔야했다"라고 생각하며 다시 대학교를 들어가서 대학생활을 하면서 졸업할 때까지 똑같이 살다가 다시 졸업하고 자신을 돌아보는 반면에 TD같은 경우는 같은 대학교를 다니고 있는 2학년 선배가 1학년선배를 이끌어주는 것을 말합니다.
사실은 둘 다 대학교를 졸업을 해보지 않은 상태에서 (잘 모르는 상황에서)이끌어 주는 것이지만 대학교를 다니면서 바로 바로 자신을 고쳐나가기 때문에 어쩌면 더 옳은 방법일지도 모릅니다. TD는 따라서 현재의 value function을 계산하는데 앞선(앞선이라고 표현하기에는 좀 애매한 부분이 있지만)주변의 state들의 value function을 사용합니다. 이 것은 이전에 배웠던 Bellman Equantion이며 따라서 Bellman equation자체가 Bootstrap하는 것이라고 볼 수 있습니다.
TD는 Monte-Carlo + DP라고 말했었습니다. 이전에 봤던 Monte-Carlo prediction에서 incremental mean을 보면 아래와 같이 return을 사용해서 update합니다. TD에서는 이 Gt를 $${ R }{ t+1 } + \gamma V({ S }{ t+1 })$$로 바꿔서 아래과 같은 식이 됩니다. Temporal Difference learning 방법에도 여러가지가 있는데 그 중에서 가장 간단한 방법은 TD(0)이고 방금 말한 방법이 바로 TD(0)입니다. $${ R }{ t+1 } +\gamma V({ S }{ t+1 })$$를 TD target이라고 부르고 그 타겟과 현재의 value function과의 차이를 TD error라고 부릅니다.
TD(0)의 알고리즘을 살펴보고 backup diagram을 보면 아래와 같습니다.
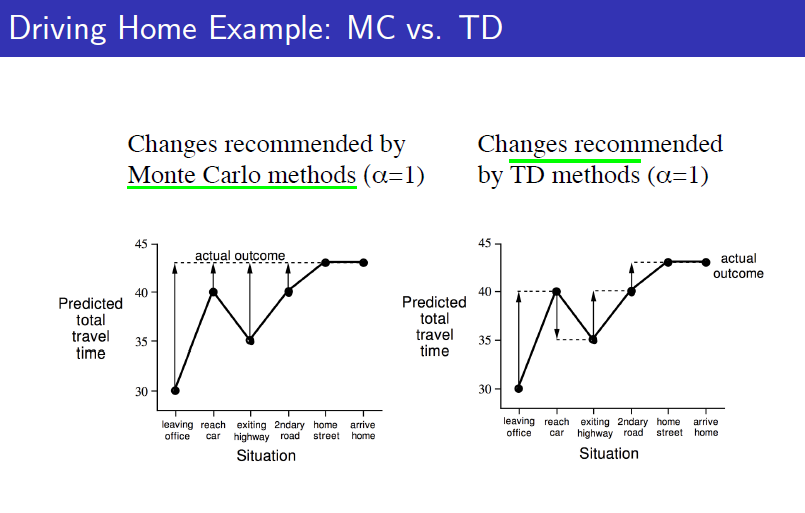
MC와 TD를 비교한 예제는 다음과 같습니다. 직장에서 집까지 가는 episode에 대한 prediction에 대한 예제인데(Control은 아닙니다) 직장에서 출발하고, 차가 막히고, 비가 오고, 고속도로를 나가고 집에 도착하고 이런 상태들을 "state"로 잡고 각각의 state에 있을 때 앞으로 얼마나 걸릴지에 대해 agent가 predict한 것에 대한 비교입니다. 그 state에서 앞으로 집으로 가기까지 얼마나 걸릴지가 value function이라 하면 각각의 상황에서 agent는 value function을 predict합니다. 그리고 state가 지날때마다 실재로 흐른 시간이 reward가 될 것 입니다.
MC의 경우에는 다 도착한다음에 각각의 state에서 예측했던 value function과 실재로 받은 return을 비교해서 update를 하게됩니다. 하지만 TD에서는 한 스텝 진행을 하면 아직 도착을 하지 않아서 얼마가 걸릴지는 정확히 모르지만 한 스텝 동안 지났던 시간을 토대로 value function을 update합니다. 따라서 실재로 도착을 하지 않아도, final outcome을 모르더라고 학습할 수 있는 것이 TD의 장점이며 매 step마다 학습할 수 있다는 것도 장점입니다.
또 한가지 중요한 차이점은 바로 bais와 variance 입니다. 이 두 개념이 무엇일까요?http://bywords.tistory.com/entry/%EB%B2%88%EC%97%AD-%EC%9C%A0%EC%B9%98%EC%9B%90%EC%83%9D%EB%8F%84-%EC%9D%B4%ED%95%B4%ED%95%A0-%EC%88%98-%EC%9E%88%EB%8A%94-biasvariance-tradeoff
아래와 같이 중앙이 있다면 중앙으로부터 전체적으로 많이 벗어나게 되면 bais가 높다, 혹은 biased됬다라고 하고 전체적으로 많이 퍼져있으면(가운데로부터 벗어난 것이랑 관계없이) variance가 높다고 합니다.
둘 다 낮으면 좋겠지만 보통은 Trade-Off관계에 있어서 하나가 낮아지면 하나가 높아지는 관계에 있습니다. TD는 bais가 높고 MC는 variance가 높습니다. 둘 다 학습에 방해가 되는 요소입니다.
TD는 한 episode안에서 계속 업데이트를 하는데 보통은 그 전의 상태가 그 후에 상태에 영향을 많이 주기 때문에 학습이 한 쪽으로 치우쳐지게 됩니다. 계속 같은 분야 사람들과 이야기를 하면 생각의 폭이 좁아지는 것과 비슷하다할까요 혹은 한 사람의 조언만 들으면 안되는 이유가 그 사람은 그 사람의 인생만 살아봤기 때문에 한 쪽으로 치우쳐질 즉, bais가 높을 수 있으니 여러 사람의 의견을 들어보는 것이 좋습니다.
하지만 너무 여러 사람의 의견을 듣다보면 이도 저도 아니게되서 결정을 못하게 되곤 합니다. 이러한 저희의 경험들이 사실 bais/variance trade-off와 관련이 되어있습니다. MC가 variance가 높은 이유는 앞에서도 설명했었지만 에피소드마다 학습하기 때문에 처음에 어떻게 했냐에 따라 전혀 다른 experience를 가질 수가 있기 때문입니다.
앞으로도 Bais와 Variance는 머리속에 기억해두어야할 게 대부분의 강화학습을 발전시키려는 노력들이 근본적인 다른 알고리즘을 채택하는 것에도 있지만 그 알고리즘의 bais와 variance를 낮추려는 것에 집중된 경향이 있기 때문입니다.
