Monte-Carlo Policy Gradient : REINFORCE
앞에서 살펴봤던 Finite Difference Policy gradient는 numerical한 방법이고 앞으로 살펴볼 Monte-Carlo Policy Gradient와 Actor-Critic은 analytical하게 gradient를 계산하는 방법입니다. analytical하게 gradient를 계산한다는 것은 objective function에 직접 gradient를 취해준다는 것입니다. 이때, Policy는 미분가능하다고 가정합니다.
이 때 gradient를 계산하는 것을 episode마다 해주면 MC Policy Gradient이고 time step마다 계산할 수 있으면 Actor-critic입니다. 밑에서 보면 score function이라는 것이 나옵니다. score function이란 무엇일까요?
1. Score Function
anaytical하게 gradient를 계산하기 위해서 Objective function에 직접 gradient를 취하면 다음과 같습니다. objective function으로 average reward formulation을 사용하였습니다. gradient를 $$\theta$$에 대해서 취하기 때문에 objective function의 식 중에서 policy에만 gradient를 취하면 되서 안쪽으로 들어가게 됩니다.

하지만 gradient가 안쪽으로 들어가면서 log가 갑자기 나오는데 그 이유는 다음과 같습니다. $$\nabla\theta \pi\theta$$에 $$\pi\theta$$를 곱하고 나누면 아래와 같이 log의 미분의 형태가 되기 때문에 $$\pi\theta$$의 gradient를 $$log\pi_\theta$$의 gradient로 바꿀 수가 있습니다.

왜 이렇게 하는 것일까요? 만약에 log의 형태로 바꾸지 않았다고 생각하면 식은 다음과 같이 됩니다.
$$\sum { s\in S }^{ }{ d(s) } \sum { a\in A }^{ }{ { { \nabla }{ \theta }\pi }{ \theta }(s,a)\quad{ R }_{ s,a }\quad } $$
이렇게 되면 $$\pi_\theta$$가 사라졌기 때문에 expectation을 취할 수가 없습니다. 결국은 expectation으로 묶어서 그 안을 sampling하게 되어야 강화학습이 될텐데 따라서 expectiation을 취하기 위해서 policy를 나눴다가 곱하는 것입니다. 그래서 score function은 아래과 같이 정의가 됩니다.

objective function의 gradient는 다음과 같습니다.

2. Policy Gradient Theorem
 이 식의 의미는 다음과 같습니다. p(x)는 policy라고 보시면 되는데$$\nabla\theta log\pi\theta$$ 는 이 policy를 표현하는 parameter space에서의 gradient입니다. 이 때 여기에 scalar인 reward r을 곱해줌으로서 어떤 방향으로 policy를 업데이트해줘야 하는지를 결정합니다. 따라서 그 방향으로 parameter space에서의 policy가 이동하게 됩니다.
http://karpathy.github.io/2016/05/31/rl/
이 식의 의미는 다음과 같습니다. p(x)는 policy라고 보시면 되는데$$\nabla\theta log\pi\theta$$ 는 이 policy를 표현하는 parameter space에서의 gradient입니다. 이 때 여기에 scalar인 reward r을 곱해줌으로서 어떤 방향으로 policy를 업데이트해줘야 하는지를 결정합니다. 따라서 그 방향으로 parameter space에서의 policy가 이동하게 됩니다.
http://karpathy.github.io/2016/05/31/rl/

이 때, policy가 어디로 얼만큼 update 될 것인지의 척도가 되는 scalar function으로 immediate reward만 사용하면 그 순간에 잘했냐, 잘 못했냐의 정보밖에 모르기 때문에 제대로 학습이 되지 않을 가능성이 높습니다. 이 immediate reward대신에 자신이 한 행동에 대한 long-term reward인 action-value function을 사용하겠다는 것이 olicy Gradient Theorem입니다. 따라서 아래의 마지막 식을 보면 r대신에 Q function이 들어간 것을 볼 수 있습니다. 한 순간 순간의 reward를 보는 것이 아니라 지금까지 강화학습이 그래왔듯이 long-term value를 보겠다는 것입니다. 이 Theorem은 Sutton교수님의 "Policy Gradient Methods for Reinforcement Learning with Function Approximation"논문에 증명되어있습니다.

3. Stochastic Polciy
위의 gradient를 통해서 policy의 parameter들을 업데이트할 것입니다. 하지만 그 전의 stochastic한 policy를 어떻게 표현할 수 있을까요? 보통 딥러닝에서 output node에서 많이 사용되는 nonlinear함수인 Sigmoid함수와 Softmax함수를 많이 사용합니다.
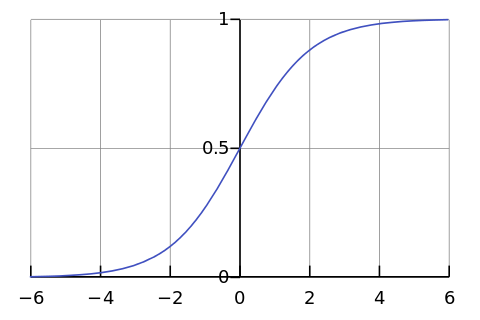
Sigmoid Sigmoid함수는 다음과 같이 표현됩니다.https://en.wikipedia.org/wiki/Sigmoid_function $$S(t)={\frac {1}{1+e^{-t}}}$$ 이 함수를 그래프로 나타내면 다음과 같습니다. 이 함수는 output이 0~1사이의 값으로 나오는 함수입니다. 따라서 stochasitc 즉 확률을 나타내는 데에는 좋습니다. discrete action space의 경우agent가 왼쪽과 오른쪽으로 갈 수 있다면(action = left, right) 이 함수에서 나오는 값이 "1에 가깝다면 왼쪽으로 갈 확률이 높고 0에 가깝다면 오른쪽으로 갈 확률이 높다"라는 식으로 설정하여 stochastic한 policy를 표현할 수 있습니다. 또는 continuous action space일 경우에는 다른 형태로 표현할 수도 있습니다. 만약 어떤 로봇의 controller에 0부터 100까지 control input을 줄 수 있다면 sigmoid함수를 통해 0이 나오면 control input은 0, 1이 output으로 나오면 control input은 100을 주는 식으로 설정하면 continuous action또한 표현할 수 있습니다.
Softmax 만약 discrete action space에서 action이 3개 이상이 되면 sigmoid함수로 표현하기가 애매해집니다. 이럴 때는 Softmax함수를 쓰는 것이 좋습니다. Softmax함수는 다음과 같이 표현할 수 있습니다. https://en.wikipedia.org/wiki/Softmax_function action이 i=1부터 n까지 있을 때 각각의 action probability를 위의 함수로 표현할 수 있습니다. agent가 두 가지 행동을 한 번에 할 수는 없으므로 위 식이 좋은 건 모든 action probability를 더하면 1이 된다는 점입니다.

이렇게 stochastic한 policy를 어떻게 표현하는 지, sigmoid와 softmax에 대해서 간단히 설명했는데 사실 이론보다는 실재로 코드로 구현할 때 해보면 더 잘 이해가 될 것 같습니다.
4. Monte-Carlo Policy Gradient
여기까지 policy gradient를 통해서 학습을 할 준비는 끝냈습니다. objective function을 정의했고 policy를 parameter를 통해서 나타났을 때 그 parameter를 update하기 위해서 objective function의 gradient를 구해야 했습니다. objective function의 gradient는 아래와 같이 정의됩니다. 하지만 action value function의 값을 어떻게 알 수 있을까요? 이전에 모든 state에 대해 action value function을 알기 어려워서 approximation을 했었는데 policy자체를 update하려니 기준이 필요하고 그러다보니 action value function을 사용해야하는데 사실 이 값을 알 방법이 애매합니다.

하지만 알 수 있는 방법이 있는데 바로 Monte-Carlo방법입니다. episode를 가보고 받았는 reward들을 기억해놓고 episode가 끝난 다음에 각 state에 대한 return을 계산하면 됩니다. return자체가 action value function의 unbiased estimation입니다. 이러한 알고리즘은 REIFORCE라고 하며 아래와 같습니다.

loop문을 보시면 학습, 즉 parameter의 update가 episode마다 일어나고 있음을 알 수 있습니다. 이 때 parameter를 regression방법이 아니고 stochastic gradient descent방법을 사용해서 한 스텝씩 update합니다.
results matching ""
Last updated