Neural Network

1. What is DQN

강화학습에서 agent는 environment를 MDP를 통해서 이해를 하는데 table 형태로 학습을 모든 state에 대한 action-value function의 값을 저장하고 update시켜나가는 식으로 하면 학습이 상당히 느려집니다. 따라서 approximation을 하게되고 그 approximation방법 중에서 nonlinear function approximator로 deep neural network가 있습니다. 따라서 action-value function(q-value)를 approximate하는 방법으로 deep neural network를 택한 reinforcement learning방법이 Deep Reinforcement Learning(deepRL)입니다. 또한 action value function뿐만 아니라 policy 자체를 approximate할 수도 있는데 그 approximator로 DNN을 사용해도 DeepRL이 됩니다.

action value function을 approximate하는 deep neural networks를 Deep Q-Networks(DQN)이라고 하는데 그렇다면 DQN으로 어떻게 학습할까요? DQN이라는 개념은 DeepMind의 "Playing Atari with Deep Reinforcement Learning"라는 논문에 소개되어있습니다. https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf

2. Artificial Neural Networks (ANN)

http://sanghyukchun.github.io/74/ deepRL을 하려면 딥러닝의 기본적인 개념에 대해서 알 필요가 있습니다. 위 블로그에 게시된 내용을 바탕으로 관련내용을 요약해봤습니다. 저 또한 딥러닝은 처음 접하는 것이라 앞으로도 공부가 필요할 것 같습니다. 강화학습이 사람의 행동방식을 모방했다라고 한다면, artificial neural networks(줄여서 neural networks)는 사람의 뇌의 구조를 모방했습니다. 인공지능이 사람의 뇌를 모방하게 된 것에는 컴퓨터가 계산과 같은 일에는 사람보다 뛰어난 performance를 내지만 개와 고양이를 구별하는 사람이라면 누구나 간단하게 하는 일은 컴퓨터는 하지 못했기 때문입니다. 따라서 이미 뇌의 구조에 대해서는 수많은 뉴런들과 시냅스로 구성되어있다는 것을 알고 그것을 수학적 모델로 만들어서 컴퓨터의 알고리즘에 적용시키는 방법을 택한 것입니다.

neural networks의 수학적 모델에 대해서 간단히 살펴보겠습니다. 그 전에 사람의 뉴런의 구조를 보면 http://arxiv.org/pdf/cs/0308031.pdf

각 Neuron들은 synapse를 통해서 signal을 받습니다. 만약 signal이 어떤 특정한 threshlod를 넘어간다면 neuron이 activate되고 그 뉴런은 axon을 통해서 signal을 다른 synapse로 보냅니다. 이러한 구조를 뉴런의 모양을 빼고 process위주로 다시 표현을 해보면 다음과 같습니다. http://www.slideshare.net/imanog/artificial-neural-network-48027460

시냅스를 통해서 input이 들어오면 뉴런은 processs를 진행하고 output을 내놓습니다. process는 input이 들어가서 output이 나오는 일종의 함수입니다. 지금은 단순히 하나의 input에 하나의 output만을 적었지만 사실은 여러개의 input이 들어와서 여러개의 output이 나가는 데 그 input과 output은 뉴런 사이의 연결을 통해서 전달됩니다. 그러한 구조를 다시 그림으로 표현하자면 다음과 같습니다.

이 그림에서와 같이 뉴런의 시냅스가 10개라고 가정해보면 이 시냅스들을 통해서 10개의 다른 input들이 들어오게 됩니다. 뉴런의 process에 들어가는 값은 이 10개의 input들의 linear combination입니다. 이 process를 거친 y값은 다시 다른 뉴런들의 시냅스로 input으로 들어가게 됩니다. 이러한 사람의 뉴런의 구조를 모방해서 인공신경망을 구성하면, 각 neuron들은 node가 되고 synapse를 통해서 들어오는 signal은 input이 되고 각각 다른 synapse를 통해서 들어오는 signal들의 중요도가 다를 수 있으므로 weight를 곱해줘서 들어오게 됩니다. 이 signal들이 weight와 곱해진 것이 위에서 언급했던 net input signal입니다. 그 net input signal을 식으로 표현해보자면 다음과 같습니다.

시냅스로 들어오는 각각의 input을 vector로 표현하고 그 input에 각각 곱해지는 weight 또한 그에 따라 vector로 만들어서 두 vector를 곱해서 input과 weight의 linear combination을 만들어줍니다. 여기서 새로운 개념이 나타나는데 b로 써지는 bias입니다.

Bias가 linear combination에 더해져서 net input signal로 들어가는 이유는 간단하게 말하자면 다음과 같습니다. 좌표평면에서 (0,0)과 (5,5)을 어떠한 선을 기준으로 구분하고 싶다고 생각해봅시다(예를 들면, 고양이과 개를 구분하는 문제라고 할 수 있습니다). bias가 없는 y = ax같은 함수의 경우에는 두 점을 구분할 수 있는 방법이 없습니다. 하지만 y = ax + b는 이 두 점을 구분할 수 있습니다.

또한 다른 식으로 bias의 필요성을 설명하자면 다음과 같습니다.http://stackoverflow.com/questions/2480650/role-of-bias-in-neural-networks

Modification of neuron WEIGHTS alone only serves to manipulate the shape/curvature of your transfer function, and not its equilibrium/zero crossing point. The introduction of BIAS neurons allows you to shift the transfer function curve horizontally (left/right) along the input axis while leaving the shape/curvature unaltered. This will allow the network to produce arbitrary outputs different from the defaults and hence you can customize/shift the input-to-output mapping to suit your particular needs.

즉 노드로 들어가는 input들에 곱해지는 weight(학습시키려는 대상)을 변화시켜면 함수의 모양만 변화시킬 수 있지 왼쪽/오른쪽으로 이동시켜서 0이 되는 point를 변형시킬 수는 없습니다. 따라서 bias를 사용하면 사용자의 요구에 더 유동적으로 그래프를 이동 및 변형시켜서 학습할 수가 있습니다.

input signal들과 weight가 곱해지고 bias가 더해진 net input signal이 node를 activate시키는데 그 형식을 function으로 정의할 수 있습니다. 그러한 함수를 activation function이라 합니다. 이러한 개념들을 모두 합해서 그림으로 나타낸 artificial neuron은 다음과 같습니다.

f라고 표현되어 있는 activation function의 가장 간단한 형태는 들어온 input들의 합이 어떤 Threshold보다 높으면 1이 나오고 낮으면 0이 나오는 형태일 것입니다. 하지만 이런 형태의 activation function의 경우에는 미분이 불가능하고 따라서 gradient descent를 못 쓰기 때문에 그 이외의 미분가능 함수를 사용합니다. gradient descent에 대해서는 뒤에서 설명하겠습니다. 밑의 사진은 activation function의 예시입니다.

위에서 말한 가장 간단한 activation function의 형태는 첫번째 그림과 같습니다. 위에서 언급했듯이 이 함수 대신에 미분가능한 함수를 사용하게 되었고 그 중에 대표적인 함수가 세번째 그래프인 sigmoid Function입니다. sigmoid function이란 무엇일까요? 식으로 다음과 같이 표현됩니다.

activation function의 예시에는 sigmoid말고도 세 가지 다른 함수들이 있는데 이 함수들은 다 non-linear합니다. 그 이유는 activation function이 linear할 경우에는 아무리 많은 neuron layer를 쌓는다 하더라도 그것이 결국 하나의 layer로 표현되기 때문입니다.

• sigmoid function

• tanh function

• absolute function

• ReLU function

가장 실용적인 activation function은 ReLU function이라고 합니다. 저희 또한 ReLU function을 activation function으로 사용했습니다. ReLU란 어떤 함수일까요? http://cs231n.github.io/neural-networks-1/

위의 왼쪽 그림처럼 x가 0보다 작거나 같을때는 y가 0이 나오고 x가 0보다 클때는 x가 나오는 함수를 ReLU(The Rectified Linear Unit)이라는 함수입니다. 위 글에 써져있듯이 최근 몇 년동안 유명해지고 있는 함수입니다. 사실 딥러닝이 최근에 갑자기 급부상한 이유는 엄청 혁신적인 변화가 있었던 것이 아니고 activation함수를 sigmoid에서 ReLU로 바꾸는 등의 작은 변화들의 영향이 크다고 볼 수 있습니다.

sigmoid함수에 비해서 ReLU함수는 어떠한 장점이 있을까요? 위 그림에서 보듯이 ReLU의 직선적인 형태와 sigmoid함수처럼 수렴하는 형태가 아닌 점이 ReLU의 stochastic gradient descent 가 더 잘 수렴하게 해줍니다. 또한 상대적으로 sigmoid함수에 비해서 계산량이 줄 게 됩니다. 장점이 있으면 단점도 있는 법입니다. 단점은 다음과 같습니다. Learning rate에 따라서 중간에 최대 40%정도의 network가 "die"할 수 있다고 합니다. 단, learning rate를 잘 조절하면 이 문제는 그렇게 크지 않습니다.

앞에서 살펴본 artificial neuron들을 network로 표현하면 위와 같습니다. 사실은 사람 뇌의 뉴런들은 이보다 상당히 더 복잡하게 연결되어 있지만 머신러닝에서 사용하는 neural network는 훨씬 간단한 형태입니다. 위에서 보이는 동그라미들은 뉴런에 해당하는 node들입니다. 이 node들은 각 층으로 분류될 수 있고 같은 층안에서는 연결되어 있지 않습니다. 정보의 방향은 왼쪽에서 오른쪽으로 흘러가는데 그렇지 않은 network도 있습니다(RNN). 보통은 node들이 fully-connected되어 있어서 한 node에서 나온 output들은 다음 층의 모든 node에 input으로 들어가게 됩니다. 왼쪽과 오른쪽은 둘 다 neural network이지만 차이는 오른쪽의 network는 hidden layer가 2층인 것을 알 수 있고 hidden layer가 2층 이상인 neural network를 deep neural network라고 부릅니다.

3. SGD(Stochastic Gradient Descent) and Back-Propagation

(1) SGD

지금까지는 deep neural network가 무엇인지에 대해서 살펴보았습니다. 다시 이 글의 처음으로 돌아가서 DQN이란 action-value function을 deep neural network로 approximation한 것을 말합니다. 강화학습의 목표는 optimal policy를 구하는 것이고 각 state에서 optimal한 action value function을 알고 있으면 q값이 큰 action을 취하면 되는 것이므로 결국은 q-value를 구하면 강화학습 문제를 풀게됩니다. 이 q-value는 DNN(deep neural networks)를 통해서 나오게 되는데 결국 DNN을 학습시키는 것이 목표가 되게 됩니다.

따라서 approximation하지 않았을 때와 다른 것은 q-table을 만들어서 각각의 q-value를 update하는 것이 아니고 DNN안의 weight와 bias를 update하게 됩니다. 그렇다면 어떻게 update할까요?

이 때 이전에 배웠던 Stochastic Gradient Descent가 사용됩니다. 정리하자면 gradient descent라는 것은 w를 parameter로 가지는 J라는 objective function을 minimize하는 방법중의 하나로서 w에 대한 J의 gradient의 반대방향으로 w를 update하는 방식을 말합니다.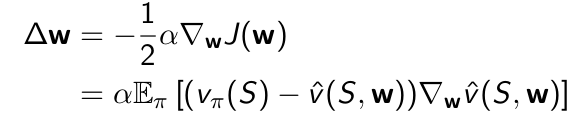

이런식으로 update를 하게되는데 모든 데이터에 대해서 gradient를 구해서 한 번 update하는 것이 아니고 sampling을 통해서 순차적으로 update하겠다는 gradient descent방법이 stochastic gradient descent입니다. 아래 페이지를 참고해보면 그렇게 할 경우 수렴하는 속도가 훨씬 빠르며 online으로도 학습할 수 있다는 장점이 있습니다. 또한 하나 중요한 점은 gradient descent방법은 local optimum으로 갈 수 있다는 단점이 있습니다. http://sebastianruder.com/optimizing-gradient-descent/

(2) Back-Propagation

이 gradient를 구했다면 DNN의 안에 있는 parameter들을 어떻게 update할까요? 다시 DNN안에서 data가 전달되어가는 과정을 생각해봅시다. input이 들어가면 layer들을 거쳐가며 ouput layer에 도달한 data가 output이 되어서 나오게 됩니다.

parameter를 SGD로 update할 때는 그 반대 방향으로 가게 됩니다. 따라서 그 이름이 Back-Propagation이라는 이름이 붙습니다. Tensorflow를 사용할 경우에는 그러한 식들이 library화 되있어서 여기서 다룰 내용은 아닌 것 같습니다.